70以上 f(x)=1/1-x^2 find domain and range 599998-30.find the domain and range of the function f(x)=(1)/(1-x^(2))
Algebra Find the Domain and Range F (x)=1/ (x^2) F (x) = 1 x2 F ( x) = 1 x 2 Set the denominator in 1 x2 1 x 2 equal to 0 0 to find where the expression is undefined x2 = 0 x 2 = 0 Solve for x x Tap for more steps Take the square root of both sides of the equation to eliminate the exponent on the left side x = ± √ 0 x = ± 0For domain under root should not be n egative quantity, 16−x2 ≥ 0 16≥ x2 Therefore, x ≤ 4 or x ≥ −4 Then, The domain−4,4 Range f (x) is maximum at x= 0,f (x)= 4 And f (x) is minimum at x= 4,f (x To find The domain and range of the real function Solution To find domain Equate the denominator to zero Denominator (3x)=0 x=3 This means at x=3 function is not defined And by definition of domain The domain is where the function is not defined Domain is Range Put f(x)=y Range is the set of value that correspond to domain

F X 1 X 2 1 Find Domain And Range Of The Following Function Brainly In
30.find the domain and range of the function f(x)=(1)/(1-x^(2))
30.find the domain and range of the function f(x)=(1)/(1-x^(2))- Find the domain and range of a function f(x)=1/(1x^2) Forums Maths, Math, Homework, Do My Homework Email this Topic • Print this Page Swapnil Reply Mon 23 Jun, 14 1144 am Find the domain and range of a function f(x)=1/(1x^2) Stumble It!If x denotes the integral part of x, then domain of the function f (x) = g (x) h (x), where g (x) = (x − 1) (x − 2) (x − 3) 3 − x and h (x) = sin − 1 2 3 x − 2 is 0, 2) − {1} Reason




Find The Range Of F X 1 1 2cosx Mathematics Topperlearning Com Qd9zj00
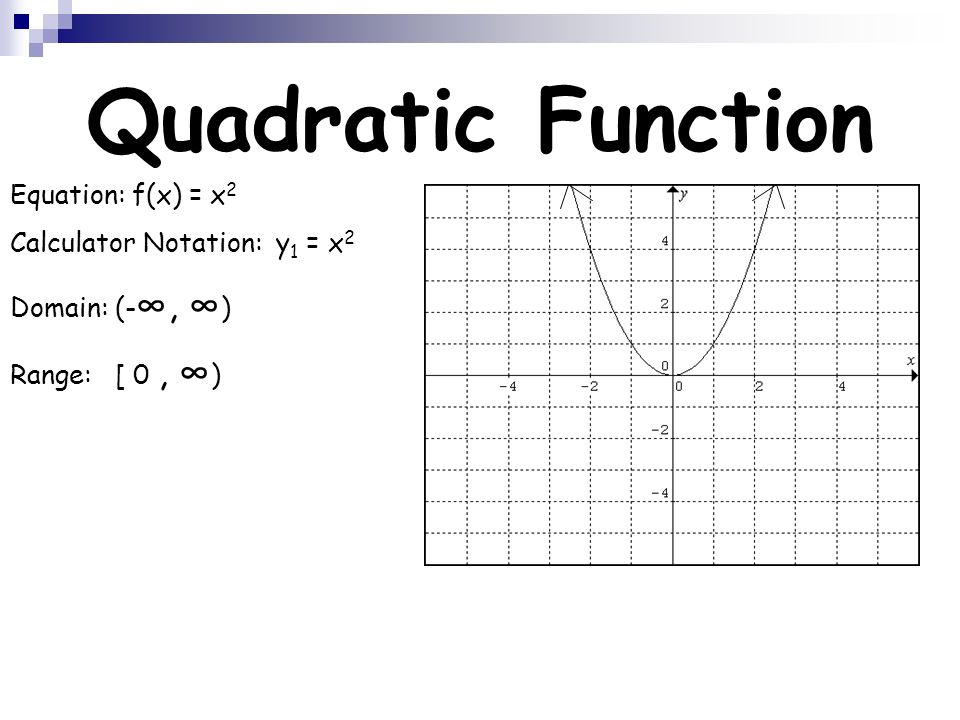
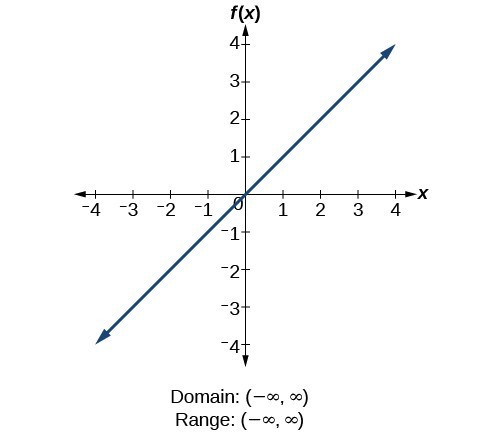
Domain of f ( x) = sin ( ln ( 1 − x 4 − x 2 )) is Medium View solution > The value of x for which the function 2 x − 5 1 is not defined Medium View solution > A = the domain of f where f ( x) = lo g x 2 and B = the domain of g where g ( x) = 2 lo g x, then A − B =The domain is easy to find The denominator must be nonzero, and the quantity being squarerooted must be nonnegative Combine these two conditions The range could cause us some trouble To begin with, note that the function is always positive, as per the definition of the square rootAlgebra Find the Domain and Range f (x)=x^21 f (x) = x2 1 f ( x) = x 2 1 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation
Find the domain and range of the following real functions f(x)=x^29/x3 asked Feb 9 in Sets, Relations and Functions by Ekaa ( 268k points) relations and functionsSo, the range is 0, ∞) Question 2 Find the domain and range of the following functions f(x) = 1 x 2 Solution For any values values of x, the function will give defined values It will never become undefined So, domain is all real values that is R The range of x 2 lies between 0 to ∞ But we need find the range of 1 xClearly, f(x) is defined for all x ∈ R except for which x2 − 1 = 0 ie, x = ± 1 Hence, Domain of f = R − { − 1, 1} Let f(x) = y Then, 1 1 − x2 = y ⇒ 1 − x2 = 1 y ⇒ x2 = 1 − 1 y = y − 1 y ⇒ x = ± √y − 1 y − 0 Clearly, x will take real values, if
To find the domain, let f(x)=1/log(2x) is not defined for 1 2xF(x)=1/(4x^21) The domain is x values in which the function is defined Since the function is a root, then the denominator (4x^21) should not be zero 2x 1 = 0 2x = 1 x = 1 / 2 Therefore , Domain = R { 1/2 } All real numbers are used as range here For getting solve the denominator of the given fraction and reduce the value of x from the real number "R" Hope it helps you dude



1




Find The Domain And Range Of The Functions G X Y Chegg Com
Find the domain and range of the function `f(x)=(1)/sqrt(x5)`Range of arccot(x) View more examples »How to Find the Domain and Range of f(x, y) = ln(xy 2)If you enjoyed this video please consider liking, sharing, and subscribingYou can also help support



Graphing The Basic Functions




Find The Range F X Root 9 X 2 My Doubt Is That The Answer Says 0 3 But Since We Have A Square Root Won 39 T We Get Range 3 3 Mathematics Topperlearning Com Zmdkzt22
The function f(x) = x 2 has a domain of all real numbers (x can be anything) and a range that is greater than or equal to zero Two ways in which the domain and range of a function can be written are interval notation and set notation Given f(x) = 1x2 To find the range of function Explanation So, the range of a function consists of all the second elements of all the ordered pairs, ie, f(x), so we have to find the values of f(x) to get the required range Given, f(x) = 1x2 Now for real value of f, x2≥ 0 Adding negative sign, we get Or x2≤ 0 AddingExample 1 Find the domain and range of the function y = 3 x 2 Graph the function on a coordinate plane The graph is nothing but the graph y = 3 x translated 2 units to the left The function is defined for all real numbers So, the domain of the function is set of real numbers



How Do You Find The Domain And Range Of Y 3x 2 Socratic




Example 15 F X 1 X What Is The Domain And Range Examples
• Tweet This • Bookmark on Delicious • Share on FacebookArithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution f(x)=\frac{1}{x^2} domain\y=\frac{x}{x^26x8} domain\f(x)=\sqrt{x3} domain\f(x)=\cos(2x5) domain\f(xThis is a revised answer!



If F X Sin Log 4 X 2 1 X Then The Domain Of F X Is Sarthaks Econnect Largest Online Education Community



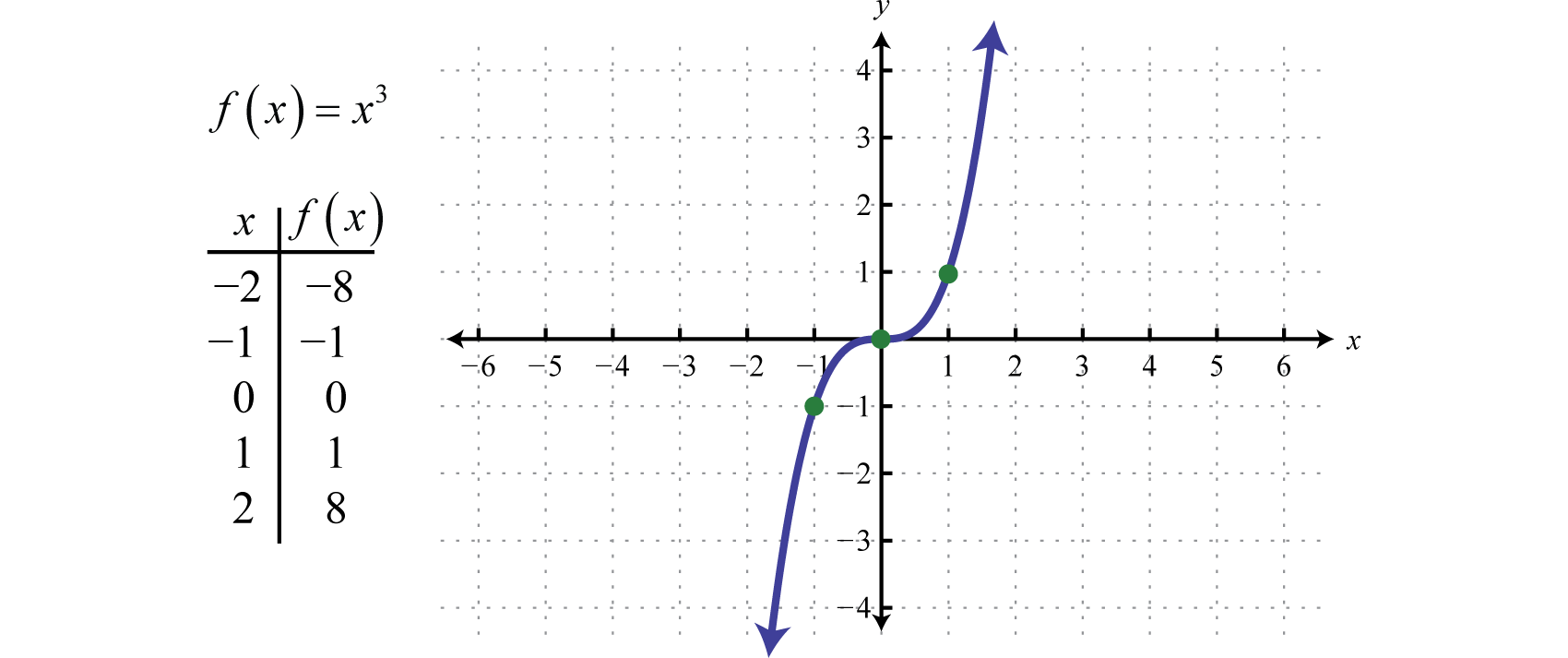
Let F Rtor F X X 3 For All X Inr Find Its Domain And Range Also Draw Its Graph
What is the domain and range of f(x)=1/sqrt (9x^2)?To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find domain and range of `f(x)=x/(1x^2)` For instance, f (x) = The domain is simply the denominator set equal to 0, {xl x≠3} However, range is found by solving for (isolating x to one side) and setting the denominator equal to zero x = So range is {xl x≠0} This is a systematic method that I assume is the only way to find the range



Find The Range F X Root 9 X 2 My Doubt Is That The Answer Says 0 3 But Since We Have A Square Root Won 39 T We Get Range 3 3 Mathematics Topperlearning Com Zmdkzt22




Calculus Practicals Maxima And Minima Derivative
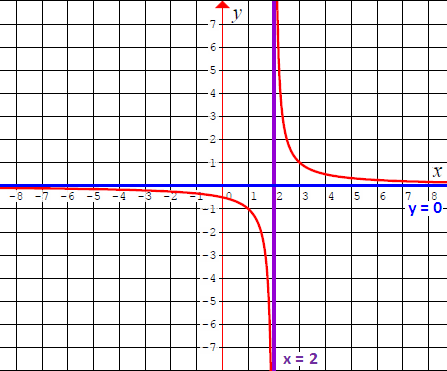
Misc 5 Find the domain and the range of the real function f defined by f (x) = x – 1 Here we are given a real function Hence, both domain and range should be real numbers Here, x can be any real number Here, f (x) will always be positive or zero Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that range f (x) is 0 or positive numbers, So range cannot be negative Hence, RangeFind the domain and range of the function f (x) = 2 − sin3x1 Solution Solution f (x) = 2 − sin3x1 Here, 2 − sin3x can never be zero as sin3x will always less than 2 ∴ Domain of f (x) will be x ∈ R Now, f (x) will be maximum when 2 − sin3x is minimum 2 − sin3x will be minimum when sin3x = 1Algebra Find the Domain and Range f (x)=1/x f (x) = 1 x f ( x) = 1 x Set the denominator in 1 x 1 x equal to 0 0 to find where the expression is undefined x = 0 x = 0 The domain is all values of x x that make the expression defined Interval Notation



Relations Functions Pps




6 Ways To Find The Domain Of A Function Wikihow
Find the range of function f(x) = cot^1(2x x^2) asked in Sets, relations and functions by SumanMandal ( 546k points) inverse trigonometric functions To answer this problem, the first thing we can consider is if there are any values, for what the function, f(x) is undifined at, this would be where the denominator =0 => 1 e^(2x) = 0 => e^(2x) = 1 => 2x = ln(1) => x = 1/2 ln(1) We know 1/2 ln(1) notin RR So hence the denominator is defined AAx in RR ( defined for all x values in the real set) We also know e^(2x) is also defined AAx in RR So hence f(x) is defined for AAx in RR Domain x in RR (for all real values of x )Domain of f (x) is − ∞, ∞) From ( 1 ), The range of f (x) = 3 x 2 7 x 1 0 is Medium View solution > If the range of the function f (x) = 6




F X 1 X 2 1 Find Domain And Range Of The Following Function Brainly In




Domain And Range Free Math Help
X, y ∈ R Let y = f (x) Then y = 1 1 − x 2 y = 1 (1 x) (1 − x) means that x ≠ ± 1 because the denominator cannot be 0 So the domain of f is {x x ≠ − 1 or x ≠ 1} To find the range, get x in terms of y y = 1 1 − x 2 y (1 − x 2) = 1 y − x 2 y = 1 − x 2 y = 1 − y x 2 y = y − 1 The domain of the function will thus be ( −∞, − 1) ∪(1, ∞) The range of the function will be determine by the fact that the square root will always give a positive value for real numbers This means that the range of the will be 0, ∞) graph {sqrt (x^21) 79, 7904, 3946, 3956} Answer linkFind the domain of 1/(e^(1/x)1) function domain square root of cos(x) log(1x^2) domain;




Homework Math Stpm Pdf



Madasmaths Com Archive Maths Booklets Standard Topics Various Function Exam Questions Pdf
Precalculus We find the domain and range of the function f(x) = 1/(x^22x8) Two approaches are used the first uses the graph of the parabola y=x^2x8, Find the domain and range of the real function f (x) = x/1x^2 ━━━━━━━━━━━━━━━━━━━━━━━━━ ️Given real function is f (x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ R Misc 4 Find the domain and the range of the real function f defined by f(x) = √((𝑥−1)) It is given that the function is a real function Hence, both its domain and range should be real numbers x can be a number greater 1 Here, f(x) is always positive, Minimum value of f(x) is 0,




Lesson 1 1 Pages 5 11 State The Domain And Range Of Each Relation Then State Whether The Relation Is A Function Write Yes Or No Pdf Free Download




Domain And Range Calculator Wolfram Alpha
Example 1 Find the domain and range of the following functions f(x) = 1/(2 sin 3x) Solution In order to find the domain, let us equate the denominator to 0 2 sin 3x = 0 sin 3x = 2 This is impossible, because the minimum value of sin is 1 and maximum value is 1For the reciprocal squared function latexf\left(x\right)=\frac{1}{{x}^{2}}/latex, we cannot divide by latex0/latex, so we must exclude latex0/latex from the domain There is also no latexx/latex that can give an output of 0, so 0 is excluded from the range as well Note that the output of this function is always positive due to the square in the denominator, so the rangeThis is a quadratic function There are no rational or radical expressions, so there is nothing that will restrict the domain Any real number can be used for x to get a meaningful output Because the coefficient of x 2 is negative, it will open downward With



3




Domain Range A Find The Natural Domain 3 1 F X Chegg Com
Step 1 Draw the graph Step 2 Find the possible values of x where f (x) is defined Here the x values start from 2 and ends in 2 Step 3 The possible values of x is the domain of the function ∴ \therefore ∴ the domain of the circle is { x ϵ R − 2 ≤ x ≤ 2 x\epsilon \mathbb {R}2\leq x\leq 2 xϵR −2 ≤ x ≤ 2 } =What are the domain and range of the realvalued function f(x) = −3x 2 6x 1? Find the domain of each of the following functions given by f(x) = (x^3 x 3)/(x^2 1) asked in Sets, Relations and Functions by RamanKumar (




1 Find The Inverse Of F Deter See How To Solve It At Qanda




How To Find The Range Of A Function Video Khan Academy
Find the Domain and Range f (x)=x^2 f (x) = x2 f ( x) = x 2 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x xEnter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask for the domain and range domain of log(x) (x^21)/(x^21) domain;Calculus Find the Domain and Range f (x)= (x1)/ (x1) f (x) = x − 1 x 1 f ( x) = x 1 x 1 Set the denominator in x−1 x1 x 1 x 1 equal to 0 0 to find where the expression is undefined x1 = 0 x 1 = 0 Subtract 1 1 from both sides of the equation x = −1 x = 1




Find The Domain And Range Of F X 1 Sin X Find Chegg Com




Exercise 1 3 Functions Problem Questions With Answer Solution
The given real function is f (x) = x − 1 It can be seen that x − 1 is defined for (x − 1) ≥ 0 ie, f (x) = (x − 1) is defined for x ≥ 1 Therefore the domain of f is the set of all real numbers greater than or equal to 1 ie, the domain of f = 1, ∞)What is the domain and range of the real function f(x)=1/(1x^2)? 1 Confirm that you have a quadratic function A quadratic function has the form ax 2 bx c f (x) = 2x 2 3x 4 The shape of a quadratic function on a graph is parabola pointing up or down There are different methods to calculating the range of a function depending on the type you are working with




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube




Tr Exercises 1 1 Functions In Exercises 1 6 Find The Chegg Com




The Problem Was To Graph The Function Find The Chegg Com




Domain And Range Of Inverse Trigonometric Functions




Find The Domain Range Of F X 1 9 X 2 Brainly In
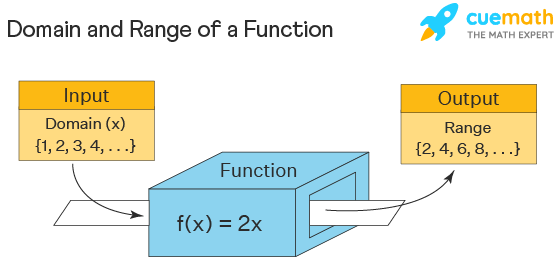



Domain And Range Examples Domain And Range Of Functions




1 Let Fx 2xa2 X 1 Evaluate O C 2 0 0 1 Chegg Com




Find The Domain And Range Of The Functions F X X2 X 1 X2 X 1 Maths Meritnation Com




Find The Domain And Range Of The Function F X X 1 X 2 Maths Relations And Functions Meritnation Com



What Is The Range Of Y X X 1 Quora




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2



What Is The Domain And Range Of X 2 1 X 2 Quora




Ex 2 3 5 Find The Range Of Function F X 2 3x X R X 0
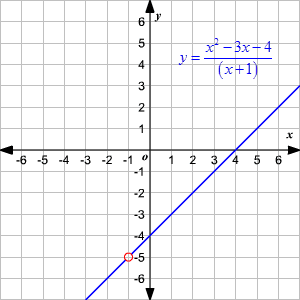



Domain And Range Of Rational Functions




Example 15 F X 1 X What Is The Domain And Range Examples



Madasmaths Com Archive Maths Booklets Standard Topics Various Function Exam Questions Pdf




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot




Find The Range Of I F X X 4 X 4 And Domain Of Ii F X 1 Log 10 1 X Sqrt X 2




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube




Answered 3x For 1 X 1 Let F X X 4 For Bartleby



What Is The Range Of F X X 2




F X Sqareroot Of Sin X Cos X Find Domain And Range Mathematics Topperlearning Com Yskun1qq
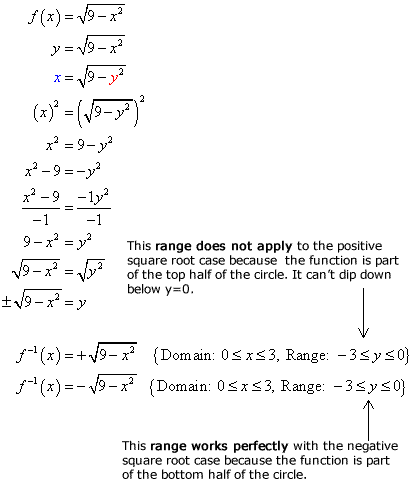



Inverse Of Square Root Function Chilimath




Consider The Real Valued Function Satisfying Math 2f Sin X F Cos X X Math The Domain Of Math F Math Is Math 1 1 Math What S The Range Of Math F Math Quora
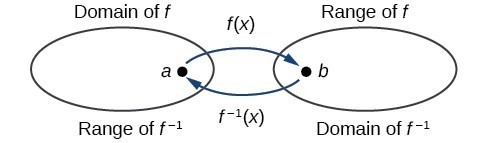



Determine The Domain And Range Of An Inverse Function College Algebra




Find The Domain And Range Of The Following Functions I F X X 2 Ii F X X 1 3 X



Q Tbn And9gcqj529kunx E23asbmwgf8sdjnucswezuevva8edino5czgfbjv Usqp Cau



What Is The Range Of The Function F X X 1 Quora



1




Important Questions For Cbse Class 11 Maths Chapter 2 Relations And Functions




Misc 3 Find Domain Of F X X2 2x 1 X2 8x 12




Domain And Range Of Functions Are Component For X And Y Values
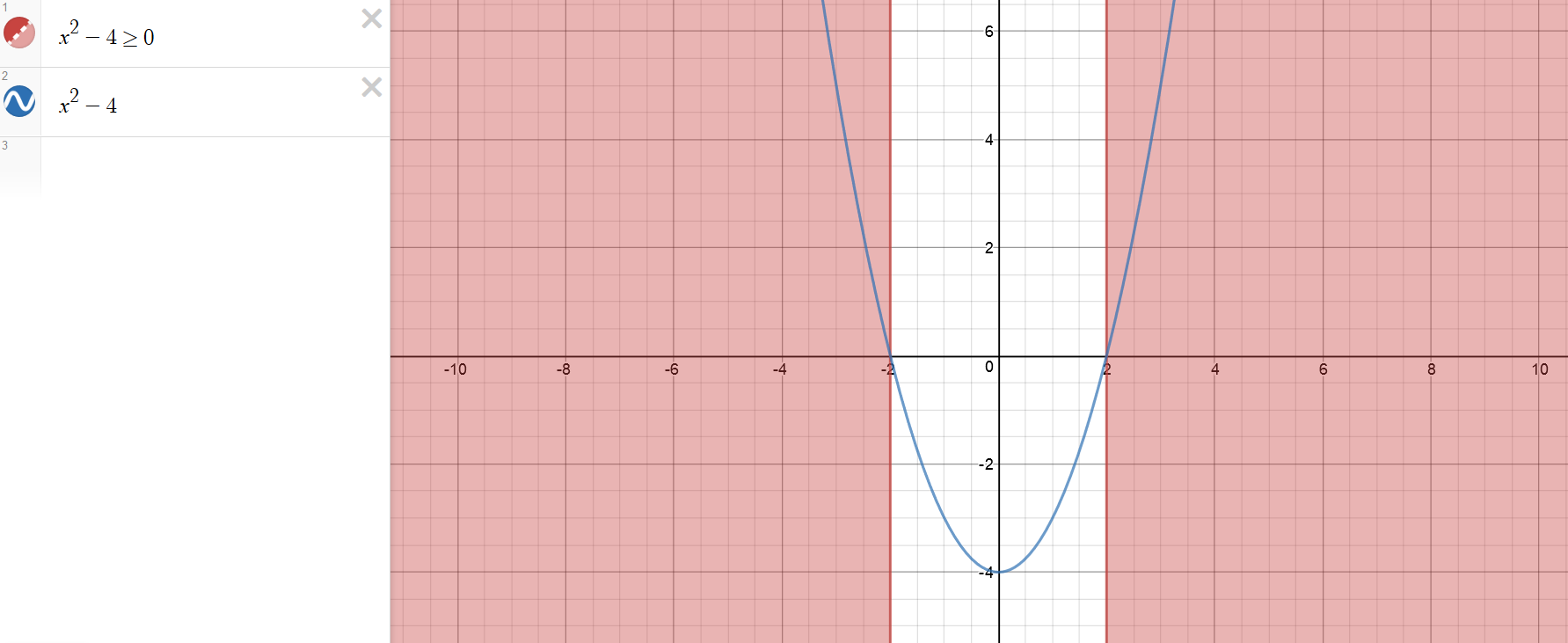



How Do You Find The Domain And Range Of Sqrt X 2 4 Socratic




Rd Sharma Solutions For Class 11 Maths Updated For 21 22 Chapter 3 Functions



Domain And Range And Composition Of Functions
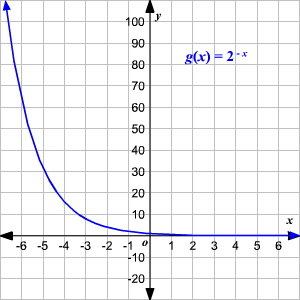



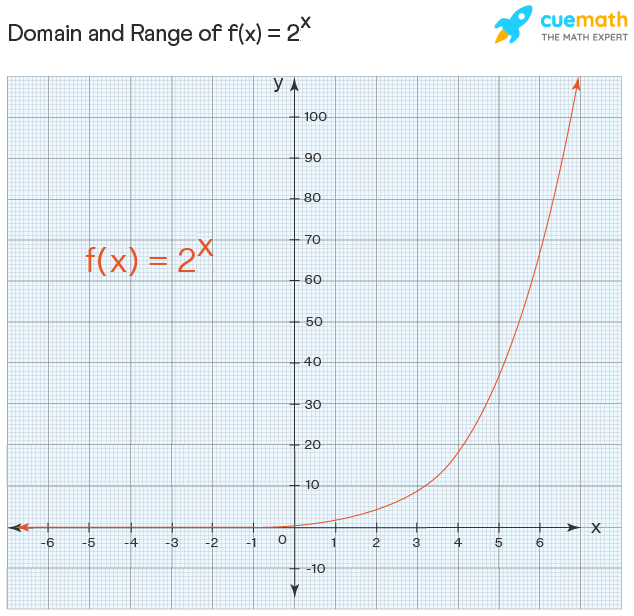
Domain And Range Of Exponential And Logarithmic Functions




Find Domain And Range F X X 1 X 1 Maths Relations And Functions Meritnation Com




Domain And Range Of Quadratic Functions Video Khan Academy




Graph The Following Functions Determine The Domain Chegg Com



Biomath Functions



Domain And Range Examples Domain And Range Of Functions



Parent Functions Learning Goal I Will Be Able To Recognize Parent Functions Graphs And Their Characteristics Ppt Download




Answered 1 Find Domain And Range Of Each Bartleby




Find The Domain And Range Of F X 1 Sqrt X 2




4 Ways To Find The Range Of A Function Wikihow




Finding Domain And Range




Find The Domain And The Range Of The Function Fleft Xright Frac X 2 X 1 X 2 X 1 Snapsolve



Find Domains And Ranges Of The Toolkit Functions Math 1314 College Algebra




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2




Find The Domain And Range Of The Real Function Fx 1 1 X 2 Brainly In




6 1 The Composition Of Functions F O G Composition Of The Function F With G Is Is Defined By The Equation F O G X F G X The Domain Is The Set Ppt Download
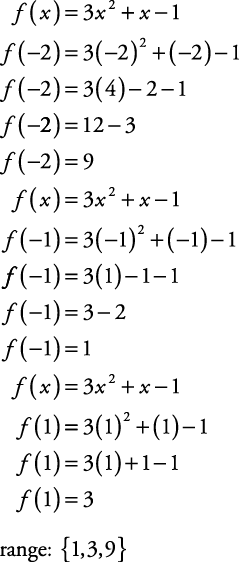



Functions




Find The Domain And Range Of Following Function F X 1 Root X Mod X Brainly In



Domain And Range Of Rational Functions




Find Domain And Range Of F X X 1 X 2




Let A 1 2 3 14 Define A Relation R From A To A By R X Y 3x Y 0 Where X Y A Write Down Its Domain Co Domain And Range
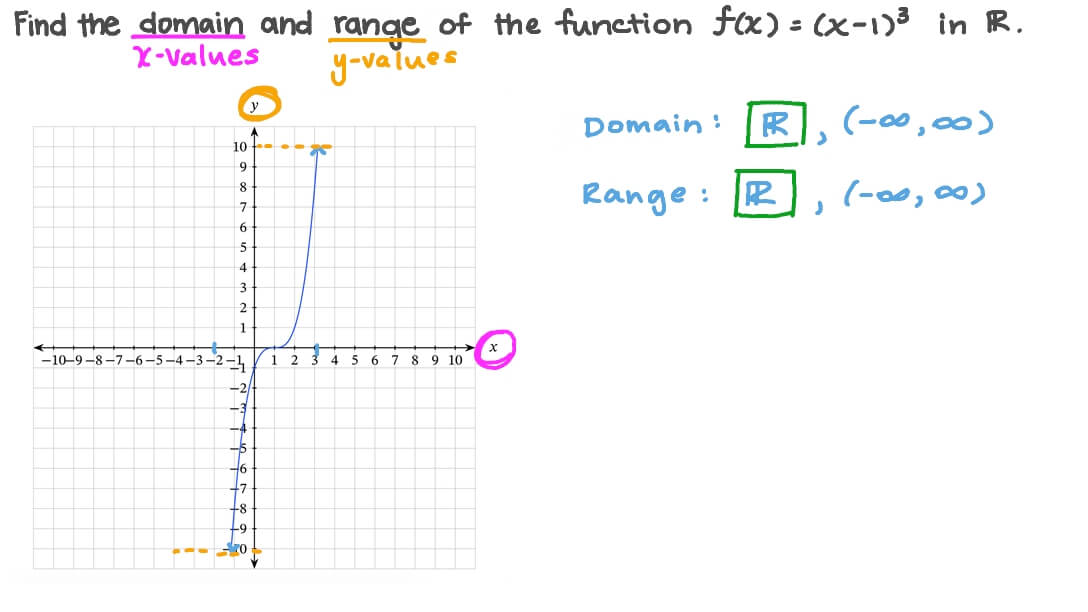



Question Video Finding The Domain And Range Of A Cubic Function Given Its Graph Nagwa



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic




How To Find Domain And Range From A Graph Video Khan Academy



Www Math Colostate Edu Clayton Teaching M113f09 Homework Hw1solutions Pdf




Misc 5 Find Domain And Range Of F X X 1 Class 11




Rd Sharma Solutions For Class 11 Maths Updated For 21 22 Chapter 3 Functions
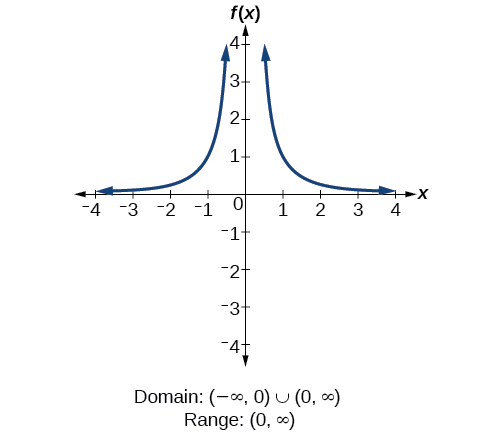



3 3 Domain And Range Mathematics Libretexts




Domain And Range Of F X X 3 X 3 Are Respectively
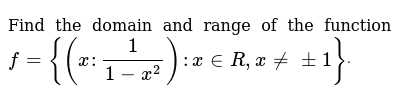



Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot



What Is The Domain And Range Of F X X 2 X 2 Quora




Lesson 3 8 Functions Ppt Download




Ncert Exemplar Class 11 Maths Chapter 2 Relations And Functions Learn Cbse




Example 15 F X 1 X What Is The Domain And Range Examples
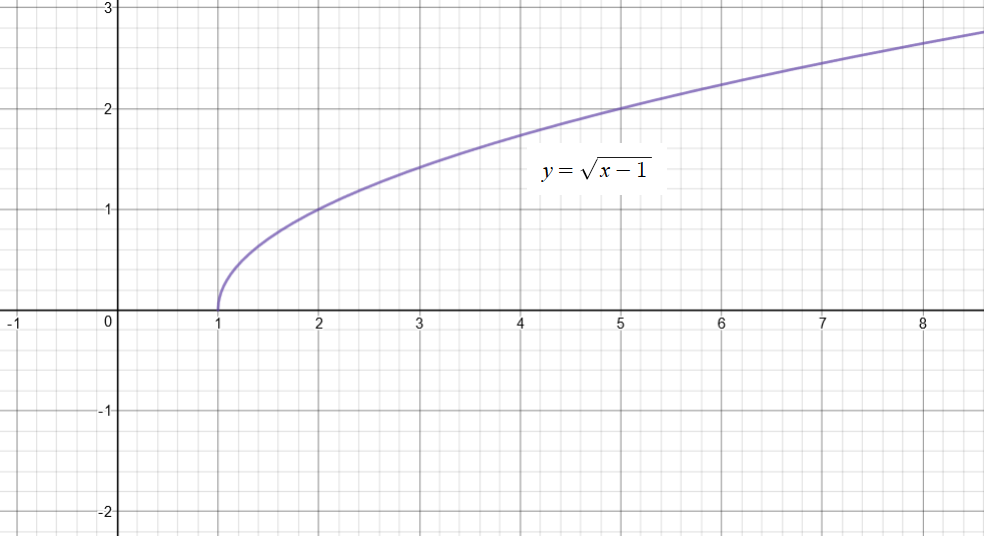



What Is The Domain And Range For F X Sqrt X 1 Socratic




Find The Range Of F X 1 1 2cosx Mathematics Topperlearning Com Qd9zj00




Inverse Of Quadratic Function Chilimath
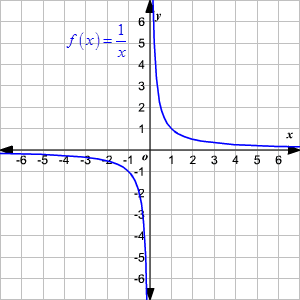



Domain And Range Of Rational Functions




Finding Domain And Range



Domain And Range Of A Function




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube




Ncert Exemplar Class 11 Maths Chapter 2 Relations And Functions Learn Cbse
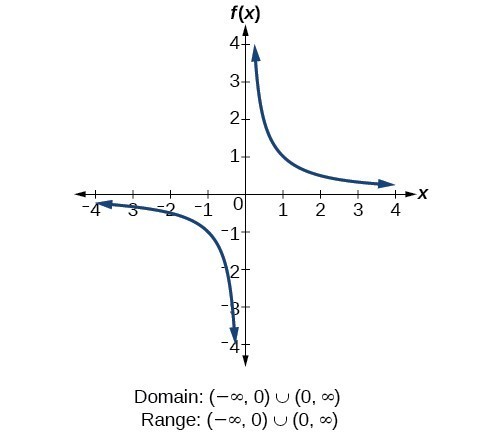



Find Domains And Ranges Of The Toolkit Functions Math 1314 College Algebra




Ws 1 1 Answer Key




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube



Comments
Post a Comment